How to cope with nested SV? - Our solution.

After finishing the aligner MA, we decided to work on an SV caller on top of it; just like Sniffles sits on top of NGMLR. We thought it would be a good start to simulate perfect alignments for various variants and use these alignments for testing our initial approach. We quickly ran into the following problem: The internal representation of SV in our caller turned out to be ambiguous; (1) one internal representation could be interpreted in several ways (One representation corresponded to multiple different sequenced genomes). (2) And, the other way around, multiple internal representations could mean the same thing (one sequenced genome corresponded to multiple representations). To give a language-based analogy: (1) The word “saw” has two meanings: “I saw my brother” and “He owns a saw”. (2) And, the other way around, there are synonyms for the word “saw” as e.g. “witnessed”, “watched”, etc. For maintaining internal consistency, these ambiguities needed to be resolved. In this blog, we describe what we came up with.

Let’s start by looking at an example: Assume that we have a reference genome that consists of three sections and as shown in Figure 1. Additionally, let’s assume that we have the following two statements: (A) “In the sequenced genome, section has been duplicated.” (B) “Section occurs inverted on the sequenced genome.”

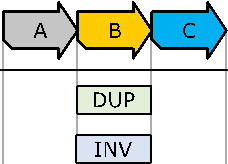
Figure 1: Two atomic SVs on a reference genome. The reference genome is visualized diagrammatically and is composed of the three sections A, B and C.

These are typical statements generated by SV calling. Further, the callers give us no knowledge about the order of application for these two statements (in fact, statements are usually simply ordered ascendingly by their reference positions). Therefore, they can be interpreted in many different forms that lead to different sequenced genomes. This corresponds to above mentioned “I saw my brother”, “he owns a saw.”-type ambiguity. Figure 2 shows the three different forms of interpretation of the duplication and inversion affecting. The three interpretations lead to the three different sequenced genomes , and .

Figure 2: Three different sequenced genomes can result from the above atomic variants (duplication & inversion) and reference genome. The inversion of sections is displayed by rotating the sections’ arrows.

Let’s now look to these sequenced genomes via dot-plots:

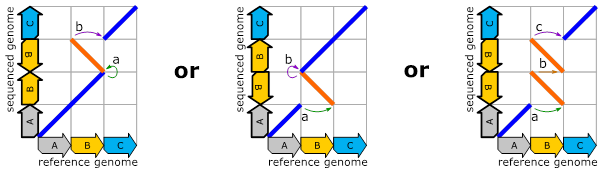
Figure 3: The outcome of the above genomic rearrangements described via diagrammatic dot-plots. Blue lines indicate equivalence between forward strand of the sequenced genome and forward strand of the reference genome. Orange lines indicate equivalence between forward strand of the sequenced genome and reverse strand of the reference genome.

Naturally, since the three sequenced genomes are different, we see three different dot-plots. This tells us that the above ambiguities can be resolved by capturing the outcome of the genomic reorganization process instead of the process itself. The dot-plots also pose a new problem though: For creating them, we need a complete assembled sequenced genome (for the y-axis). The construction of such assembled genomes is expensive and we would like to work directly with reads instead. A single read delivers a small interval of the y-axis. Sadly, the read comes without any knowledge about the location of its y-axis interval. Wouldn’t it be great to have a representation of these dot-plots without the need for the y-axis? Well, such a representation does exist and it can be achieved by focusing on “breakend-pairs”. These breakend-pairs are the positions where we have a difference between reference genome and sequenced genome. In the dot-plots, these pairs show up as positions where we “jump” or have a “change of direction”.

These breakend-pairs can be nicely stored in graphs, as shown in the figure below which corresponds to the leftmost dot-plot of Figure 3:

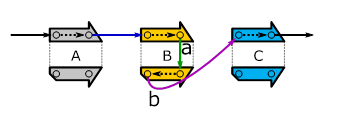
Figure 4: The outcome of the leftmost genomic rearrangement described via a graph.

These graphs can be read as follows: By following the “arrows” (called edges), we can walk along the sequenced genome. Starting from the black edge on the top-left we:

(1) walk along the forward strand of A and then follow the blue edge,

(2) walk along the forward strand of B and then follow the edge labeled a,

(3) walk along the reverse strand of B and then follow the edge labeled b and

(4) walk along the forward strand of C.

The above “traversal” creates the sequenced genome’s forward strand (). For getting the reverse strand, we have to travel in the “opposite direction” as shown below.

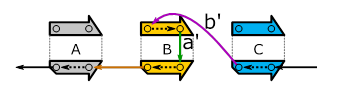
Figure 5: Same as Figure 4, but for the reverse-complement strand.

Knowing one of the above graphs means knowing the other. The relationship they have is called “skew symmetry”.

For representing graphs, we, like many others, use adjacency matrices. Because the graphs in Figure 4 and Figure 5 share the same vertices (genome sections, nucleotides), we can combine them in one adjacency matrix as shown below:

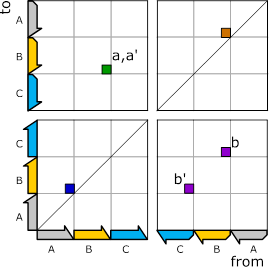
Figure 6: The above two graphs for forward and reverse strand in one adjacency matrix.

Adjacency matrices capture the edges (arrows) of graphs. They are read in a from-to fashion: A point at position indicates that there is an edge that runs from to . E.g. the point labeled with an x-position at the end of B on the reverse strand (next to the nook) and a -position at the beginning of C on the forward strand expresses the edge labeled in Figure 4 that connects these two positions. Please note that in the above adjacency matrix the forward strand and the reverse strand occur separated. Further, the matrix consists of four quadrants labeled . Entries in the first quadrant correspond to edges that connect vertices (nucleotides, genome sections) on the reverse strand. Accordingly, the third quadrant contains edges connecting forward strand vertices. And the remaining two quadrants comprise edges that cross between strands.

Now, let’s dive deeper into this matrix. The entries labeled and correspond to the same breakend-pair (one originates from the forward strand of the sequenced genome and the other originates from the reverse strand). So, if we have reads from the forward strand and the reverse strand covering this breakend-pair, they would support the same point in the matrix. However, for and , we are not that lucky anymore. Although both points (matrix entries) correspond to the same breakend-pair, they end up in different matrix positions depending on the strand of their read. This is quite disadvantageous because in the SV caller we want to combine the SV evidence from forward-strand reads and reverse-strand reads. We fix this by applying a folding scheme to the matrix that brings and together. Notably, in the context of this folding scheme, we do not need to know the strand a read originates from.

The folding exploits the skew symmetry of the graph and works as follows:

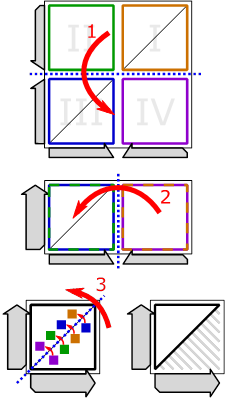
Figure 7: The folding scheme used for turning Figure 6 into Figure 7.

First, (1) fold the matrix horizontally downwards. (2) Then fold the resulting matrix vertically leftwards. And finally, (3) fold diagonally upwards. During the folding, we track the original quadrant of all entries via colors. E.g., green entries originate from the second quadrant. In the context of the final folding, we have to swap the colors of the blue and orange entries (blue entries become orange and orange entries become blue). The reasons for this swapping go beyond this blog. But, by tracing the blue and orange edges of the above example, we can see that it works. The outcome of the folding is shown below:

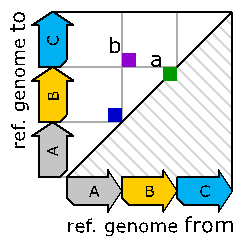
Figure 8: The adjacency matrix from Figure 6, but now information from both strands are combined.

So far, we know a folding scheme that unifies forward strand and reverse strand in the context of the matrix entries. Now, we will show how to compute the matrix entries from reads. For this blog, we assume that our reads are free of sequencing errors. Dealing with sequencing error does not require a change of the basic scheme; it merely requires some cluster considering add-ons. We explain the computation of matrix entries using a deletion as an example. Let us have a reference genome and a sequenced genome, where the sequence is deleted:

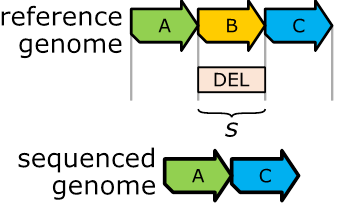
Figure 9: Section B is deleted on the reference genome.

If we express the sequenced genome in terms of the reference genome via a graph, we get the picture below:

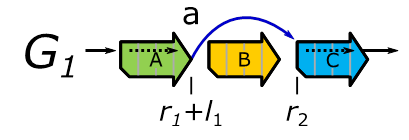
Figure 10: The sequenced genome in Figure 9, expressed as a graph.

In the edge captures the deletion of the sequence . In the reference position is connected to the reference position via the edge . This can be directly translated into an entry in the adjacency matrix as the -axis position and -axis position . The resulting matrix, denoted , is shown below:

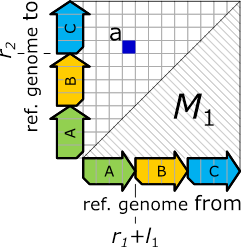
Figure 11: The graph in Figure 10, expressed as an adjacency matrix.

Now let us assume that we have a read that spans over the part of the sequenced genome that comprises the deletion. Therefore, covers the end of the sequence and some part of the beginning of . As mentioned above, this gives us a horizontal strip of the full dot-plot (for reference and sequenced genome) as shown below:

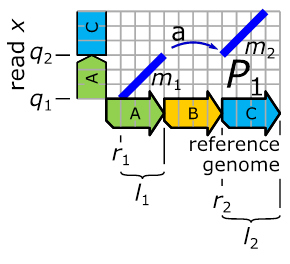
Figure 12: A horizontal strip of the full-dot plot (for reference and sequenced genome) delivered by the read .

Please note, the strip delivered by the read provides enough information for inferring the entry . In fact, the-axis position () of can be inferred from the bottom “line’s” end. The start of the upper “line” is indicating the -axis position () of . Here, the lower of two lines that occur consecutively on a read (-axis) always corresponds to the -position of an entry and the upper line always to the -position. The “lines” are simply maximal exact matches (MEMs) and, due to the folding, we do not have to worry about the reads strand.

The above scheme is fine as long as we do not have two MEMs with different reference intervals but identical (or overlapping) read intervals. I.e. does not have competing sisters like ’:

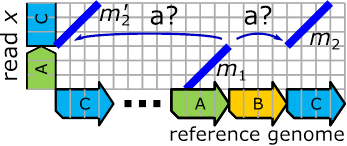
Figure 13: Repetitiveness on the reference genome – two occurrences of C.

Such situations are quite a headache-maker since we know that only one of those competing MEMs is correct and the others appear due to the repetitiveness of the reference genome. A quick fix for this problem is the application of occurrence filters that simply remove such situations. A proper solution requires further research, but we think a good approach would be a transition from the linear, sequential representation of the reference genome to a graph-based one, where the repetitiveness is resolved via the graph. In such a “world”, genomes would correspond to traversal through these graphs, where a repetitively occurring sequence in a reference genome corresponds to a repeated visit of the corresponding graph substructure.